Bitcoin transactions, metaphorically (Part 1)

If you’re reading this post it means you are alive, and if you’re alive it means you’ve probably heard about bitcoin. That in itself is quite remarkable seeing as just a few years ago pretty much the only people who had any exposure to bitcoin were the core bitcoin developers, people trading illicit substances for bitcoins on silk road, and undercover FBI agents trying to catch people trading illicit substances for bitcoins on silk road. Today silk road is gone and bitcoin is a household name making headlines almost daily. Here is one of many from Bloomberg. Even the WSJ has a dedicated bitcoin news blog called BitBeat.
So all the cool kids are talking about bitcoin these days, and we certainly don’t want to be uncool. But what are said cool kids actually talking about? We will try to answer this question, i.e. we will try to gain some understanding of the technical underpinnings of the bitcoin protocol through a series of posts.
In this first post we will give metaphors that will try to provide a heuristic, high-level understanding. A subject like bitcoin requires very strict adherence to computer security standards. It’s not reasonable for non-technical users to fully understand technical aspects like cryptographic hash functions or decentralized P2P networks, but bitcoin can be very unforgiving if you have the wrong ideas. It’s quite easy to end up doing the bitcoin equivalent of leaving a suitcase full of cash in the trunk of a taxi cab and having the taxi drive away as you get out, except in the case of the taxi there is still a chance that you might get your lost money back.
Security researcher Bruce Schneier describes how metaphors are a necessary tool to train people in computer security, and we fully agree with this. We will try to develop metaphors that are easy to grasp but at the same time maps to the correct underlying technical details. This is important because if you are using a metaphor that is not technically correct you run a real risk of losing coins, as we will see below.
Without further ado, let’s dive into our metaphors.
Addresses
An address can be thought of as an identifier that holds bitcoin. It looks something like 19fb1TrGPcJ3jwCXg7VLVoWVXTFM4oa5PB and we usually say things like “The address 19fb1Tr… has 12.4439 bitcoins in it”. You can think of the address as a safe made of indestructible glass with the identifier printed on it. All these safes are located in a public place (“the blockchain”). The public place is in a virtual environment that exists in a file that anyone can copy and share. The file is currently about 20 GB but it grows as more safes are added.
Each safe has a coin slot so anyone can insert coins if they want, and it’s transparent so everyone can see how many coins are inside. The safe has a combination lock so if you don’t know the combination you cannot access the coins inside. There is no way to reset the combination so if you forget the combination, the coins inside are inaccessible forever. There are websites where you can peruse the blockchain and look at safes, for instance our example above:
https://blockchain.info/address/19fb1TrGPcJ3jwCXg7VLVoWVXTFM4oa5PB
If we follow the link we see that this safe had 644.4612 bitcoins in it on March 26, but right now it sits empty.
Private Keys
For every address there is a corresponding private key. Think of this private key as the combination to the combination lock of the above transparent safe. The combination (private key) is a single number, but we’re not talking about a number from 1 to 100 like a regular safe; the private key is a number between 1 and where is
115792089237316195423570985008687907852837564279074904382605163141518161494337.
To get a feeling for how big this number is, if we write it in words it’s
115 quattuorvigintillion 792 trevigintillion 89 duovigintillion 237 unvigintillion 316 vigintillion 195 novemdecillion 423 octodecillion 570 septendecillion 985 sexdecillion 8 quindecillion 687 quattuordecillion 907 tredecillion 852 duodecillion 837 undecillion 564 decillion 279 nonillion 74 octillion 904 septillion 382 sextillion 605 quintillion 163 quadrillion 141 trillion 518 billion 161 million 494 thousand 337.
Technically, the number is the order of the base point of a specific elliptic curve, and we normally write it in hexadecimal as
N = FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE BAAEDCE6 AF48A03B BFD25E8C D0364141

This number is so long in hexadecimal that it doesn’t even fit on one line!
You have to be very careful with this passcode since anyone who learns it can go to the safe, open it and take the coins inside. Not only that, but if you learn a private key you can compute the corresponding address from it, so in our analogy if you have the combination to the safe you can also find the location of the safe. So private keys must be kept exactly that: private.
An interesting thing about private keys is that we can choose any number between 1 and , use it to create a safe (address) with that number as the private key and start receiving coins to that address. Anyone can have as many safes as they like, and the new safes don’t take up any space in the blockchain until some coins are deposited into them.
Intermission: Incorrect metaphors will cost you
At this point we have metaphors for addresses and private keys: Addresses are safes and keys are the combinations to the locks on those safes. A metaphor for a transaction will then be just to open your safe with the combination, take out some coins and put it in another safe, right? Wrong! If you use this metaphor you could be setting yourself up for bad things. Let’s illustrate by an example:
Suppose you randomly generate a private key, compute an address from it, and receive 1.0 bitcoins to that address from a friendly soul. Sweet, you are the proud owner of your first bitcoin! You write down the private key on a piece of paper, because you know you should not forget it since it’s the combination to your safe. You’ve also learned that if anyone else takes the key he can also take your coin, so you keep it secure at home.
Now let’s assume you want to give some coins, say 0.25 BTC, to a friend who bought you dinner the other day. You download the standard Bitcoin Core client and you import your private key into it. This makes it so that the software can open the safe and send coins on your behalf. Your software says you have 1.0 BTC. You then use the software to send 0.25 BTC to your friends address. The software now says you have 0.75 BTC. Your (incorrect but plausible) metaphor says that you’ve taken 0.25 BTC from your safe and deposited it into your friends safe, leaving 0.75 BTC in your safe.
Let’s now say you need to sell your computer, so you erase everything on the harddrive to make sure that no one else can read your personal information (including your private key). This should be fine, you think, since your 0.75 BTC is in your safe and you have the combination written down on a piece of paper. You get a new computer and you want to send some coins to another of your friends, so you import your private key into your software. Here comes the shocker: The software says that your safe is empty! Was it a thief or a hacker? Neither! You got bitten by your incorrect metaphor. To show how this happened we move on to the next section: a better metaphor for transactions.
Transactions
We’ve learned about addresses and private keys, which in our metaphor corresponds to safes with coins in them and their combinations. How are coins transferred between safes? To answer this question we need to look more closely at the safes.
The coins in a safe are divided up into trays. There is at least one tray in each safe, the trays usually hold a varying amount of coins, and trays can also be empty. The technical term for trays with coins in them is unspent outputs. The empty trays are called spent outputs.
A transaction (here I should really say standard transaction) is a ritual that is performed to move coins between safes. It is done in the following way: First we take a number of trays with coins in them (unspent outputs) from one or more safes. In order to do this we will need the private keys to open these safes.

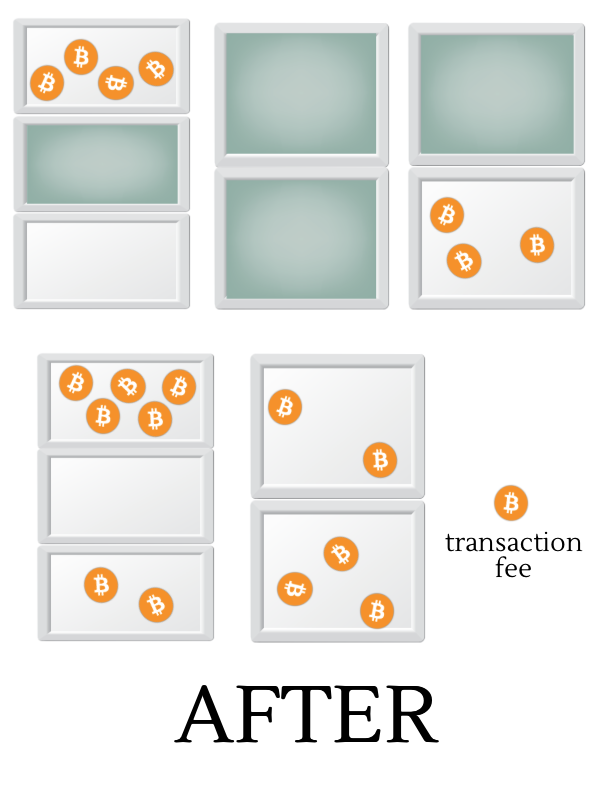
In the illustration above we wish to send coins from the three safes on top (with six, four and five coins respectively) to the two other safes. The selected trays are marked in green. We empty out all the coins from the trays into a pile on the floor, 8 coins in our example. The now empty trays are put back in their respective safes. Then we take the coins from the pile and distribute the coins inside to the other safes, five to the left safe and two to the right. We don’t need the private keys to add coins to a safe, and whenever we add coins to a safe a new tray is created to hold these coins.
Normally we leave some coins on the floor, one coin in the example above, when we’re done distributing the coins to the safes. The coins remaining on the floor are called transaction fees and are left as a gratuity for the volunteers (“miners”) who do the bookkeeping to record the transaction and help maintain the public space where the safes are stored. All transactions are meticulously recorded and kept forever for everyone to see.
Here is a real transaction recorded on the blockchain:
https://blockchain.info/tx/0b2ef83c8a895ca3ad95efa9dd50fde0fc93ac6c4447869acbf88f7c3853bb22
At this point you should be able to understand much of what is on this page. This is a transaction from the two addresses (I shorten the address labels for clarity) 18zGy and 19D9p to the five addresses 1Em12, 1C8Yu, 1maQZ, 15nFV and 146BV. If you don’t see any numbers next to the addresses 18zGy and 19D9p you need to click on “Show scripts & coinbase”. In this transaction we take a tray containing 0.18 BTC from 18zGy and a tray containing 1.53 BTC from 19D9p, dump out these coins in a pile of 1.71 BTC (called “Total Input”) and then distribute the coins to the five addresses as follows:
1Em12: 0.7253 BTC
1C8Yu: 0.0128 BTC
1maQZ: 0.8674532 BTC
15nFV: 0.050193 BTC
146BV: 0.0540538 BTC
Total: 1.7098 BTC
We see that 1.71 - 1.7098 = 0.0002 BTC is left on the floor as a transaction fee.
The transaction ritual above seems quite cumbersome. How do we create a simple transaction, for instance to pay a friend back for dinner? In this case we would gather up trays in our safes until we exceed the amount owed for the dinner, deposit the dinner money in our friends safe, and deposit the leftover coins (“change”) in a safe that we own. Often our software will create a brand new safe for us and deposit the change there (the core bitcoin client does this).
We now have enough knowledge about transaction to do a post-mortem and figure out what went wrong in the Intermission section above where we managed to lose all our coins because we were using the wrong metaphor. We have our address, let’s call it 1XXX and we received a transaction of 1.0 BTC to it. At this point there is one tray in our safe, containing 1.0 BTC. When we import the private key into the bitcoin software and send 0.25 BTC to our friends address, the following happens: Suppose our friend has address 1YYY. The software creates a transaction that will take our tray with 1.0 BTC, deposit 0.25 BTC into 1YYY, then create a new address 1ZZZ and deposit 0.75 in that address. (I pay no transaction fee in this example. This is allowed but not recommended.) Your original address 1XXX now has zero balance, and 1ZZZ has a balance of 0.75 which shows up as the balance in the client.
The problem is now that the private key for 1ZZZ is in the software client, so we need to make a backup of the software after the transaction to make sure our coins are not lost. In our example we thought that our coins were all in 1XXX, which lead to our misfortune when we erased the harddrive containing the private key for 1ZZZ.
Epilogue
The main goal of this post was to develop a good intuition for addresses, private keys, and transactions. This is needed to avoid pitfalls in thinking that can lead to lost coins. The sections above should provide pretty good intuition to avoid these pitfalls but I wanted to end with a light introduction to some slightly more advanced fun stuff.
Mommy, where do bitcoins come from?
Performing a transaction ritual as described above is the only way to transfer coins between safes, and we notice that every tray with coins came from a transaction. So where do the coins come from originally? Coins are created and given away in a raffle to the volunteers maintaing the public space and keeping the books. The volunteers are given raffle tickets in relation to how much work they do. The harder they work the more raffle tickets they get. Every 10 minutes a raffle winner is drawn and a special transaction ritual is held, called a coinbase transaction, where coins (currently 25 bitcoins) are created and deposited in the safe belonging to the raffle winner. The raffle winner also gets the transaction fees collected since the previous raffle. Here is one such coinbase transaction. The volunteers are called “miners” and bitcoin mining is a huge subject in itself that we won’t get into here.
Pimp my safe
Most addresses are like the safes described above, i.e. they have one combination lock that we unlock with our private key. There are also some safes out there with two or three combination locks. These can be programmed so that they can be opened for instance only if all the combinations are entered, or for a safe with three locks when two out of the three combinations are entered. These special safes are called multisignature addresses and people have recently been thinking about innovative ways of using these. One example is to resolve disputes in e-commerce. Suppose we want to buy some alpaca socks from an online vendor. We send our coins to a two-of-three multisignature address with three locks where we hold one key, the vendor holds another key and an independent arbitrator holds the third key. If the socks arrive and are nice and warm as expected, we along with the vendor have two keys and can together create a transaction to send the coins to the vendor without having to involve the arbitrator. If there is a dispute the arbitrator will decide if who is in the right. If the arbitrator decides that we are right, the arbitrator and us can create a transaction refunding our purchase. If the arbitrator decides that the vendor is right, the arbitrator and the vendor will create a transaction passing the funds along to the vendor. Normally the arbitrator would only charge a fee if his services are needed.
blog comments powered by Disqus