Bitcoin transactions, technically (Part 2)
In our previous post we introduced bitcoin transactions by using the metaphor of safes and coins, in order to develop an intuitive sense of the concept. Here we will investigate bitcoin transactions from a more technical standpoint using the Python bitcoin library pybitcointools, by exploring the transaction data structures directly.
As an example we will be using a real transaction which we selected randomly from the blockchain. The transaction can be viewed here:
https://blockchain.info/tx/dbebe45e62…
The reader is encouraged to look at the transaction above and cross-check the information there with what we investigate below.
Preliminaries
Here we go over some preliminaries. As we discussed in our previous post, a bitcoin private key is any number between 0 and , where is close to . From a private key we can derive a public key which is used to verify that a message has been signed by the private key. If we hash the public key by first using SHA256 and then RIPEMD160 we obtain what’s known as the Hash160 of the public key. This hash can then be written in a format called Base58Check to get the address. This format uses base 58 together with some checksums for validation reasons. Here is an example in Python:
>>> import pybitcointools
>>> privkey = pybitcointools.random_key()
>>> privkey
'34030ce14e32ac982419b3683af3b59d64a29cc93798cf479d610af49d425d13'
>>> pubkey = pybitcointools.privtopub(privkey)
>>> pubkey
'04ce0ed35340803b0c21f2f7f5d5ab9d687e5fa95a79471c9b5c9d97a0bb170eac1045230cc51d13b85a5f64feb80f8fc19358a396797926e3f89d49066b1abc07'
>>> h160 = pybitcointools.hash160(pubkey.decode('hex'))
>>> h160
'1558c7cd9825447a31990ff964f347bb2dbfe9be'
>>> addr = pybitcointools.hex_to_b58check(h160)
>>> addr
'12wsYc4B9c9JeREqstLZXNWa3n4i42M5jg'
When we describe the amount of funds to send in the low-level protocol we always use an integer amount of the unit satoshi which is named after Satoshi Nakamoto, the pseudonymous creator of Bitcoin. The satoshi is the smallest possible currency unit in bitcoin and we have that 1 bitcoin equals satoshi.
Structure of Transactions
A bitcoin transaction is a data message which in its raw form is a string of bytes like this:
>>> tx = \ '0100000002a0ae9d839ed51c9d6d299b2b3c508b935858371b283bcb1e953bc776f61c6c75000000008c493046022100b999de2e23127ec2edf16e2f267b4c2df57b9766059369cee85cbc0a41be6882022100d09c405f825eec986ca2bf6f35d1267ad7d595042fca4b4f7af3f9adfea68d330141040bf69616981e5970c992a0762f441abcadfed9fc4630fa5e1b82ab00e81d16905d3820e073e1bd4a9dcfed336f4bf25edc634c2e174989767d299748359c2dafffffffff52be06c2c43c4d0ec3c208b8b8ddbcb32ac4fdb3481addfb90498267df3ba07b010000008b48304502201193da6f0c1b3f15497415fd75743439374939191331bd7ca1ac183580ad4273022100e435bd3c48929d9789810634af47a0461e684dd490132a9c5757af86296ce0d70141046cc9eeffe66726abb725d191537f87c023202eb13ede9031d7adb80ecb0ddc9aa380cb2659747b850ea577cf04f01248ca9291976523a94ef0a907e6bb15bd55ffffffff02e0c03b00000000001976a914e1e1ffc33423807d6914de976738bbdc01477c2d88ac8c2e0100000000001976a91419e75cce5ff697a01e14ec3ebcc9a4523e44caf188ac00000000'
The above byte string encodes a data structure which contains a number of data fields. Using pybitcointools we can deserialize the structure and look at the fields:
>>> import pybitcointools, pprint
>>> tx_structure = pybitcointools.deserialize(tx)
>>> pprint.pprint(tx_structure)
{'ins': [{'outpoint': {'hash': '756c1cf676c73b951ecb3b281b375858938b503c2b9b296d9d1cd59e839daea0',
'index': 0},
'script': '493046022100b999de2e23127ec2edf16e2f267b4c2df57b9766059369cee85cbc0a41be6882022100d09c405f825eec986ca2bf6f35d1267ad7d595042fca4b4f7af3f9adfea68d330141040bf69616981e5970c992a0762f441abcadfed9fc4630fa5e1b82ab00e81d16905d3820e073e1bd4a9dcfed336f4bf25edc634c2e174989767d299748359c2daf',
'sequence': 4294967295},
{'outpoint': {'hash': '7ba03bdf67824990fbdd1a48b3fdc42ab3bcddb8b808c2c30e4d3cc4c206be52',
'index': 1},
'script': '48304502201193da6f0c1b3f15497415fd75743439374939191331bd7ca1ac183580ad4273022100e435bd3c48929d9789810634af47a0461e684dd490132a9c5757af86296ce0d70141046cc9eeffe66726abb725d191537f87c023202eb13ede9031d7adb80ecb0ddc9aa380cb2659747b850ea577cf04f01248ca9291976523a94ef0a907e6bb15bd55',
'sequence': 4294967295}],
'locktime': 0,
'outs': [{'script': '76a914e1e1ffc33423807d6914de976738bbdc01477c2d88ac',
'value': 3916000},
{'script': '76a91419e75cce5ff697a01e14ec3ebcc9a4523e44caf188ac',
'value': 77452}],
'version': 1}
Let’s take a look at the keys in the above dictionary. The key version is always 1. The key locktime is an integer specifying that the transaction is only valid after a certain amount of time has passed. This feature is very seldom used so we won’t go into it in detail. When locktime is not used the integer is set to 0. The important keys are ins, denoting a list of transaction inputs and outs denoting a list of transaction outputs. More on these below.
Transaction Outputs
Each transaction output corresponds in our previous metaphor to placing a number of coins in a safe with a particular address. The data structure has two fields:
-
value: The number of satoshis to tranfer to the destination address.
-
script: a byte string encoding the destination address.
The script encodes the destination address of this particular output as follows:
'script': 76a914e1e1ffc33423807d6914de976738bbdc01477c2d88ac
The highlighted string is the Hash160 of the public key of the destination address, as described in the Preliminaries section above. We can write it using Base58Check to obtain the address:
>>> pybitcointools.hex_to_b58check('e1e1ffc33423807d6914de976738bbdc01477c2d')
'1MbMmrTQKMc8Rm6NEV3p3bvppJGfPfiwxy'
Thus we see that the transaction will transfer 3916000 satoshis to the
address 1MbMmr. The extra bytes 76, a9, 14, 88, ac in the
script are called OpCodes, and are part of the general scripting
language of bitcoin. For standard transactions these will
always be the same, so we won’t discuss them further. In an upcoming
post we will explore this scripting language in more detail.
Transaction Inputs
Each transaction input corresponds in our previous metaphor to a tray of coins in a safe and also encodes a proof that the person requesting to move the coins has the private key to the safe. The field sequence is used in conjunction with the locktime field. This is commonly not used and when not used it’s set to . The important fields are outpoint and script, described below. We will use the transaction input with index 0 to illustrate.
Outpoint
The outpoint consists of the hash of a previous transaction and an index of the list of transaction outputs of that transaction.
'outpoint': {'hash': '756c1cf676c73b951ecb3b281b375858938b503c2b9b296d9d1cd59e839daea0',
'index': 0}
From this information we can determine the address from which to send and how many satoshis to send, in the following way: The above transaction is recorded in the blockchain and can be seen here. By looking up the transaction in the blockchain we can verify that the value of the transaction output at index 0 is 3916000. If we look up the script in the transaction output at index 0 we obtain the Hash160
script: '76a9142e1f4284e90d3e240373ec1a4b86c657749342cc88ac'
from which we can compute the address
>>> h160 = '2e1f4284e90d3e240373ec1a4b86c657749342cc' >>> pybitcointools.hex_to_b58check(h160) '15CsXoAjmPq84HVEdPR487B9ufvztYi9wq'
Thus the data in outpoint represents moving 3916000 satoshis from
address 15CsXoAjmPq84HVEdPR487B9ufvztYi9wq. Since we are requesting
to move funds from this address, we need to verify that we are the
rightful owner of this address and this is done in the below
script data field.
Script
This data field contains the necessary data to validate that the transaction author has the private key that allows her to spend the funds from the outpoint address.
The script data field consists of two parts. The second part is
the public key of the address 15CsXo of the outpoint
transaction. The first part is often denoted sig and is a message
signed with the private key corresponding to the address 15CsXo.
The message is a modified version of the total transaction structure and is created in the following way: First take the full transaction data structure, set all the input scripts to empty strings, except the current input script (index 0 in our example). The current script is set to the transaction output script of the outpoint transaction.
Let’s consider the input script in detail:
'script': '493046022100b999de2e23127ec2edf16e2f267b4c2df57b9766059369cee85cbc0a41be6882022100d09c405f825eec986ca2bf6f35d1267ad7d595042fca4b4f7af3f9adfea68d330141040bf69616981e5970c992a0762f441abcadfed9fc4630fa5e1b82ab00e81d16905d3820e073e1bd4a9dcfed336f4bf25edc634c2e174989767d299748359c2daf',
The first byte 49 denotes the length of the sig, i.e.
bytes. After the next 73 bytes there is a byte 41, denoting the
length of the public key, and we also highlight the next 65 bytes
corresponding to the public key.
Let’s verify that the 65-byte string above really is the public key. Take the string and compute the Hash160 of it followed by a Base58Check encoding:
>>> input = '040bf69616981e5970c992a0762f441abcadfed9fc4630fa5e1b82ab00e81d16905d3820e073e1bd4a9dcfed336f4bf25edc634c2e174989767d299748359c2daf'
>>> h160 = pybitcointools.hash160(input.decode('hex'))
>>> h160
'2e1f4284e90d3e240373ec1a4b86c657749342cc'
>>> pybitcointools.hex_to_b58check(h160)
'15CsXoAjmPq84HVEdPR487B9ufvztYi9wq'
We see that we’ve computed the correct Hash160 and address, so we have identified the public key in the script.
The verification of the transaction is done as follows: First the Hash160 of the public key is computed and checked to be equal to the Hash160 in the outpoint transaction output. This step is what we did above, and proves that the public key we provide is the correct one. The next step consists of using the public key to check the signature of the signed truncated transaction data structure. If this signature checks out it proves that the creator of the transaction possesses the private key required to spend the funds.
Let’s check that the sig in the script was really signed with the
private key of the address 15CsXo.
>>> sig = '3046022100b999de2e23127ec2edf16e2f267b4c2df57b9766059369cee85cbc0a41be6882022100d09c405f825eec986ca2bf6f35d1267ad7d595042fca4b4f7af3f9adfea68d3301' >>> pub = '040bf69616981e5970c992a0762f441abcadfed9fc4630fa5e1b82ab00e81d16905d3820e073e1bd4a9dcfed336f4bf25edc634c2e174989767d299748359c2daf' >>> tx_structure['ins'][0]['script'] = '76a9142e1f4284e90d3e240373ec1a4b86c657749342cc88ac' >>> tx_structure['ins'][1]['script'] = '' >>> txmod = pybitcointools.serialize(tx_structure) >>> pybitcointools.ecdsa_tx_verify(txmod, sig, pub) True
We’ve successfully verified that the modified transaction structure was indeed signed with the private key.
Moreover, since the whole transaction is signed a malicious actor cannot change the destination addresses encoded in the transaction outputs after the transaction has been sent to the network.
Chains of transactions
As we see in the transaction structure above the transaction outputs become inputs to other transactions down the line, via the outpoint field in the transaction input. This creates a chain of transactions as illustrated here:
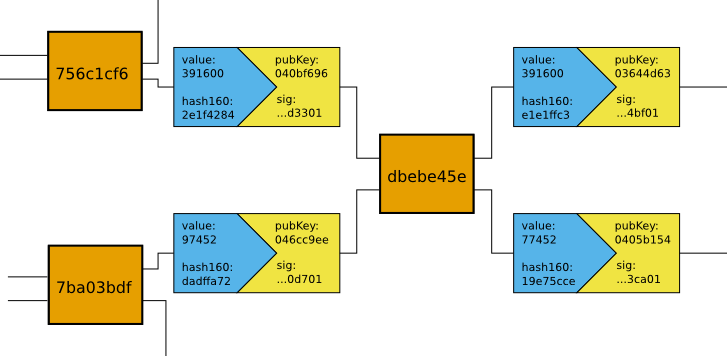
The data in these interlocking transactions is enough to trace the movements of all funds all the way from the first transaction. Thus the bitcoin network does not explicitly need to keep track of addresses and their balance, since the balance of any address can be calculated from all past transactions.
blog comments powered by Disqus